Како израчунати електрични набој

Садржај

• Формула за електрично пуњење
• Електрично пуњење и гравитација: Сличности
• Очување електричне пуњења
• Број електрона у пуњењу
• Израчунавање електричне пуњења у круговима
• Формула електричног поља
• Нето набој универзума
• Израчунавање електричног тока са пуњењем
• Пуњење и статичка електрична енергија
• Електрични проводници
• Гауссов закон у другим ситуацијама

Било да је статички електрицитет одабран крзненим капутом или електрична енергија која напаја телевизоре, о електричном набоју можете сазнати разумевањем основне физике. Начини израчунавања набоја овисе о природи саме електричне енергије, попут принципа како се набој расподјељује кроз предмете. Ови принципи су исти без обзира где се налазите у свемиру, чинећи електрични набој основним својством саме науке.

Формула за електрично пуњење

Постоји много начина израчуна наелектрисање за разне недостатке у физици и електротехници.

Цоуломбс закон се обично користи када се израчунава сила која потиче од честица које носе електрични набој и једна је од најчешћих једначина електричне наелектрисања коју ћете користити. Електрони носе појединачни набој −1.602 × 10^-19 цоуломби (Ц) и протони носе исту количину, али у позитивном смеру, 1,602 × 10 ⁻¹⁹ Ц. За две оптужбе к₁ и к₂ _ које су раздвојене растојању _р, можете израчунати електричну силу Ф_Е генерисано коришћењем Цоуломбсовог закона:

Ф_Е = фрац {кк_1к_2} {р ^ 2}

у којима к је константа к = 9.0 × 10 ⁹ Нм² / Ц². Физичари и инжењери понекад користе променљиву е да се односи на наелектрисање електрона.

Имајте на уму да је за набоје супротних знакова (плус и минус) сила негативна и самим тим привлачна између два набоја. За два набоја истог знака (плус и плус или минус и минус), сила је одбојна. Што су већа набоја, јача је привлачна или одбојна сила између њих.

Електрично пуњење и гравитација: Сличности

Цоуломбосов закон има упечатљиву сличност са Невтоновим законом за гравитациону силу Ф_{Г ​} = Г м₁м₂ / р² за гравитациону силу Ф_Г, масе м₁и м₂, и гравитациона константа Г = 6.674 × 10 ⁻¹¹ м³/ кг с². Обе мере различите силе, варирају са већом масом или набојем и зависе од полупречника између оба објекта до друге снаге. Упркос сличностима, важно је запамтити гравитационе силе увек су привлачне, док електричне силе могу бити привлачне или одбојне.

Такође требате приметити да је електрична сила генерално много јача од гравитације засноване на разликама у експоненцијалној снази константи закона. Сличности између ова два закона су већи показатељ симетрије и образаца међу уобичајеним законима универзума.

Очување електричне пуњења

Ако систем остане изолован (тј. Без контакта са било чим другим ван њега), уштедеће трошкове. Очување наплате значи да укупна количина електричног набоја (позитивног набоја минус негативног набоја) остаје иста за систем. Очување набоја омогућава физичарима и инжењерима да израчунају колико се наелектрисања креће између система и њихове околине.

Овај принцип омогућава научницима и инжењерима да стварају Фарадаиеве кавезе које користе метални штит или премаз како би спречили да набој истекне. Фарадаиеви кавези или Фарадаиеви штитници користе тенденцију електричног поља да поново дистрибуирају набоје унутар материјала како би поништили ефекат поља и спречили да набоји оштете или уђу у унутрашњост. Користе се у медицинској опреми као што су машине за магнетну резонанцу, како би се спречило изобличење података, као и у заштитној опреми за електричаре и људе који раде у опасним окружењима.

Можете израчунати нето проток набоја за запремину простора тако што ћете израчунати укупну количину уноса набоја и одузети укупну количину напуњеног трошка. Кроз електроне и протоне који носе набој, наелектрисане честице се могу створити или уништити како би се уравнотежиле према очувању набоја.

Број електрона у пуњењу

Знајући да је набој електрона –1.602 × 10 ⁻¹⁹ Ц, набој од -8 × 10 ⁻¹⁸ Ц би био састављен од 50 електрона. Ово можете пронаћи тако што делите количину електричног набоја на величину набоја једног електрона.

Израчунавање електричне пуњења у круговима

Ако знате то електрична струја, проток електричног набоја кроз објекат, путује кроз круг и колико дуго се струја примењује, можете израчунати електрични набој користећи једначину за струју К = То у којима К је укупни набој измерен у цоуломбс, Ја је струја у амперима и т је време за примену струје у секунди. Такође можете да користите Охмов закон (В = ИР) за израчунавање струје од напона и отпора.

За склоп напона 3 В и отпора 5 Ω који се примењује 10 секунди одговарајућа струја која је резултат је Ја = В / Р = 3 В / 5 Ω = 0,6 А, и укупно би пуњење К = То = 0,6 А × 10 с = 6 Ц.

Ако знате потенцијалну разлику (В) у волтима примењеним у кругу и раду (В) у џуловима урађеним током периода на који се примењује, набој у цоуломбама, К = В / В.

Формула електричног поља

••• Сиед Хуссаин Атхер

Електрично поље, електрична сила по јединици набоја, шири се радијално према ван од позитивних наелектрисања према негативним наелектрисањима и може се израчунати са Е = Ф_Е / к, у којима Ф_Е је електрична сила и к је набој који производи електрично поље. С обзиром на то колико су основно поље и сила израчунавање електричне енергије и магнетизма, електрични набој може се дефинисати као својство материје која узрокује да честица има силу у присуству електричног поља.

Чак и ако је нето или укупно наелектрисање на неком предмету нула, електрична поља омогућавају да се набоји дистрибуирају на различите начине унутар објеката. Ако унутар њих постоје расподјеле набоја, које резултирају не-нултим нето набојем, ти су објекти поларизовано, и набој који ове поларизације изазивају је познат као ограничени трошкови.

Нето набој универзума

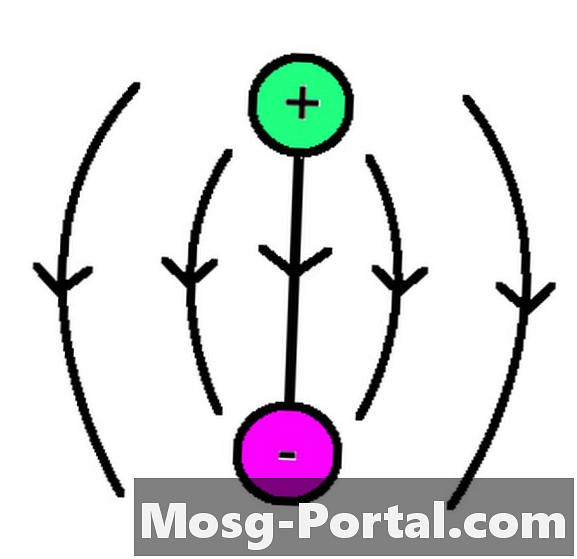
Иако се научници не слажу у томе колики је укупни набој универзума, они су разним методама смислили и тестирали хипотезе. Можете приметити да је гравитација доминантна сила у свемиру на космолошкој скали и, пошто је електромагнетна сила много јача од гравитационе силе, ако би универзум имао нето набој (позитиван или негативан), били бисте у могућности да види доказе о томе на тако великим даљинама. Непостојање ових доказа навело је истраживаче да верују да је свемир неутралан.

Да ли је свемир увек био наелектрисан или како се набој свемира променио од великог праска такође су питања која треба расправљати. Да је свемир имао нето набој, научници би требали бити у стању да мере своје тенденције и ефекте на све линије електричног поља на такав начин да се уместо повезивања са позитивних наелектрисања у негативне набоје никада не би завршили. Одсуство овог запажања такође указује на аргумент да свемир нема нето набој.

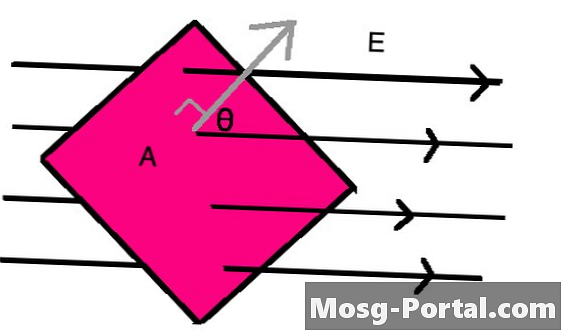
Израчунавање електричног тока са пуњењем

••• Сиед Хуссаин Атхер

Тхе електрични ток кроз равнинско (тј. равно) подручје А електричног поља Е је поље помножено са компонентом подручја окомито на поље. Да бисте добили ову окомиту компоненту, користите косинус угла између поља и равнине која вас занима у формули за флукс, представљену са Φ = ЕА цос (θ), где θ је угао између линије која је окомита на област и правца електричног поља.

Ова једначина, позната као Гауссс Лав, такође вам говори за површине попут ових, које ви називате Гауссове површине, било који нето набој стајао би на његовој површини равнине јер би било потребно створити електрично поље.

Пошто то зависи од геометрије површине површине која се користи за израчунавање флукса, то варира у зависности од облика. За кружно подручје, подручје флукса А би било π_р_² са р као полумјер круга, или за закривљену површину цилиндра, било би подручје флукса Цх у којима Ц је обим кружног лица цилиндра и х је висина цилиндара.

Пуњење и статичка електрична енергија

Статички електрицитет настаје када два објекта нису у електричној равнотежи (или електростатичка равнотежа), или да постоји нето проток наплате од једног објекта до другог. Док се материјали трљају једни о друге, они преносе набоје један између другог. Трљање чарапа на тепих или гума надуваног балона на вашој коси може створити ове облике електричне енергије. Шок враћа те вишак наплате да би се поново успоставило стање равнотеже.

Електрични проводници

За проводник (материјал који преноси електричну енергију) у електростатичкој равнотежи, електрично поље унутра је нула, а нето набој на његовој површини мора остати у електростатичкој равнотежи. То је зато што, уколико постоји поље, електрони у проводнику би се поново дистрибуирали или поново поравнали као одговор на поље. На овај начин отказали би свако поље чим би га створили.

Алуминијска и бакрена жица су уобичајени материјали проводника који се користе за пренос струја, а често се користе и јонски проводници, који представљају решења која користе слободно лебдеће јоне да би пуњење лако пролазило. Полпроводници, попут чипова који омогућавају рачунарима да раде, такође користе слободно кружеће електроне, али не онолико колико то раде проводници. Полпроводници попут силицијума и германија такође захтевају више енергије да би наелектрисање могло да циркулише и обично има ниску проводљивост. За разлику од тога, изолатори попут дрвета, не пуштају да набој лако пролази кроз њих.

Без унутрашњег поља, за Гауссову површину која лежи управо унутар површине проводника, поље мора бити свугде нуто тако да је флукс нула. То значи да унутар проводника нема електричног набоја. Из овога се може закључити да се за симетричне геометријске структуре попут сфера набој равномерно распоређује на Гауссовој површини.

Гауссов закон у другим ситуацијама

Будући да нето набој на површини мора остати у електростатичкој равнотежи, свако електрично поље мора бити окомито на површину проводника да би материјал могао да преноси набоје. Гауссов закон омогућава израчунавање величине овог електричног поља и флукса за проводник. Електрично поље унутар проводника мора бити нула, а споља мора бити окомито на површину.

То значи да за цилиндрични проводник са пољем које зрачи од зидова под правим углом, укупни ток је једноставно 2_Е__πр_² за електрично поље Е и р радијус кружног лица цилиндричног проводника. Такођер можете описати нето набој на површини користећи σ, тхе густина наелектрисања по јединици површине, помножено са површином.