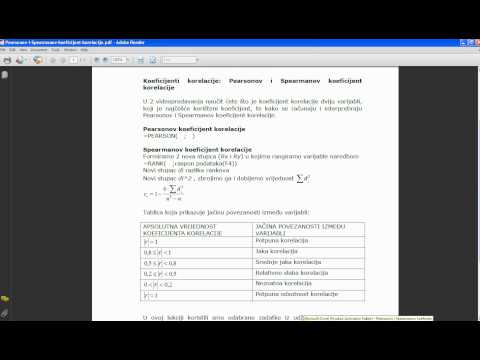
Корелација између две променљиве описује вероватноћу да ће промена једне променљиве изазвати пропорционалну промену друге променљиве. Висока повезаност између две променљиве сугерира да деле заједнички узрок или је промена једне од променљивих директно одговорна за промену друге променљиве. Вредност Пеарсонс р користи се за квантификацију корелације између две дискретне променљиве.
Означите променљиву за коју верујете да узрокује промену друге променљиве као к (независна променљива) и другу променљиву и (зависну променљиву).
Конструишите табелу са пет ступаца и онолико редова колико има тачака података за к и и. Означите колоне од А до Е са леве на десно.
У сваки ред попуните следеће вредности за сваку (к, и) тачку података у првом ступцу - вредност к у колони А, вредност к квадрат у колони Б, вредност и у колони Ц, вредност од и квадратно у колони Д, а вредност к пута и у колони Е.
Направите завршни ред на самом дну табеле и ставите зброј свих вредности сваког ступца у одговарајућу ћелију.
Израчунајте продукт крајњих ћелија у колони А и Ц.
Помножите коначну ћелију у колони Е с бројем података.
Одузмите вредност добијену у кораку 5 од вредности добијене у кораку 6 и подвуците одговор.
Помножите крајњу ћелију ступца Б с бројем података. Од ове вредности одузмемо квадрат вредности коначне ћелије колоне А.
Помножите коначну ћелију колоне Д са бројем тачака података и одузмите квадрат вредности крајње ћелије колоне Ц.
Помножите вредности пронађене у корацима 8 и 9 заједно, а затим узмите квадратни корен резултата.
Вредност добијену у кораку 7 (треба подвући) поделите на вредност добијену у кораку 10. Ово је Пеарсонс р, такође познат као коефицијент корелације. Ако је р близу 1, постоји јака позитивна корелација. Ако је р близу -1, постоји јака негативна корелација. Ако је р близу 0, постоји слаба корелација.